Why take the Rock-Scissors Challenge?
This Challenge looks at the concept of strategic thinking.
By playing multiple games of Rock-Scissors, you and your team will discover some basic mathematical methods that will help you play the game better and maybe even lead you to develop optimal strategies for bargaining, dealing and decision making.
Watch Verity introduce the Rock-Scissors Challenge.
Connections to real life
Strategic thinking is very important in the field of economics. Economists study the production and distribution of resources, goods, and services by collecting and analysing data, researching trends, and evaluating economic issues.
Using these strategies, economists, banks and governments make decisions which impact our lives on a daily basis.
1. Setting the Scene
Your family is about to embark on a very strange game of ‘Rock, Paper, Scissors’.

- You may only choose ‘Rock’ or ‘Scissors’.
- Depending on the combination of choices you make, you will get a different reward.
- Often there is often no clear winner.
After playing the game try to define the strategy that usually works the best.
Links to the curriculum
Maths words
accuracy – the probability that your shot will hit another player.
Find more maths words in the Glossary.
2. The Challenge
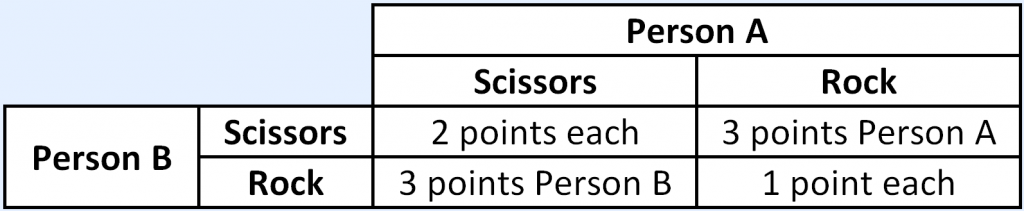
Play ‘a first to 15 points game’ of ‘Rock-Scissors’ where points are given using the table below.
1. Grab a piece of paper and a pen.
2. Split into groups of two. If you have uneven numbers you can swap partners after a game to 15 points is finished. They don’t take long.
3. The game works the same as ‘Rock, Paper, Scissors’ except you can only play rock or scissors. Instead of rock beating scissors, in this game, you receive points based on the table below. Don’t discuss the points table until after you have finished.
4 After each round keep a tally of the score.
5. Play until someone reaches 15 points.
- If both players choose ‘Scissors’ then they each get two points.
- If both players choose ‘Rock’ each player gets one point.
- If one player chooses ‘Scissors’ and the other person chooses ‘Rock’, then the person who chose ‘Rock’ gets three points (and the person who chose ‘Scissors’ gets 0 points.
Discuss: Was there any outcome that came up more often than the others? Have a look at the table again and discuss what the best strategy is to definitely beat your opponent. Is there a strategy that allows both players to win?
Advice
If you are stuck, here are suggestions that might help.
Before you play have a look at the rewards table and think about what your best option is. Remember to consider what you think your opponent will do.
You could play with a reward other than points to make the game more interesting.
3. Keep going
You find yourselves engaged in a three player laser tag duel. Read on!
1. Gather together a minimum of three people. Only three people can play at a time but you can rotate very quickly.
2. Grab three small pieces of paper, on the first piece write 33%, on the second write 67%, and 100% on the last.
3. Randomly distribute one of the pieces of paper to each person. This will be their ‘accuracy’. Make sure other players can see your piece of paper.
4. If you have 33% accuracy or 67% accuracy grab a 6-sided die each. If you dont have dice you can use this website instead.
5. Stand in a triangle 2 metres apart.
6. On the count of three, point at another player.
7. If you have 100% accuracy, you hit the person you pointed at and they are out.
8. If you have 33% accuracy, roll a die. If you roll a 1 or a 2, you hit.
9. If you have 67% accuracy, roll a die. If you roll a 1, 2, 3 or a 4, you hit.
10. Because turns happen simultaneously you can both be hit and hit someone in the same round
11. Continue playing until one person remains standing or everybody is hit. If you are the only person who hasn’t been hit, you win the round.
Discuss: What do you think the best strategy is for each person? How about if the probability is changed to: 17%; 50%; and 100% – would you change your strategy?